Medidas em Química

Medidas em Química e o Sistema Internacional de Unidades (SI)

Traduzido e adaptado de OpenStax. Acesso livre em https://openstax.org/books/chemistry-atoms-first-2e/pages/1-introduction

As medições fornecem muitas das informações que fundamentam as hipóteses, teorias e leis que descrevem o comportamento da matéria e da energia nos domínios macroscópico e microscópico da química. Cada medição fornece três tipos de informação: o tamanho ou magnitude da medição (um número); um padrão de comparação para a medição (uma unidade); e uma indicação da incerteza da medição. Embora o número e a unidade sejam explicitamente representados quando uma quantidade é escrita, a incerteza é um aspecto do resultado da medição que é mais implicitamente representado e será discutido posteriormente.

Ao final deste artigo, você será capaz de:

• Explicar o processo de medição
• Identificar as três partes básicas de uma quantidade
• Descrever as propriedades e unidades de comprimento, massa, volume, densidade, temperatura e tempo no SI
• Executar alguns cálculos de unidades básicas e conversões no sistema métrico e outros sistemas de unidades

Um número na medição pode ser representado de diferentes maneiras, incluindo forma decimal (convencional) e notação científica. (A notação científica também é conhecida como notação exponencial; trataremos disso em um artigo específico.) Por exemplo, o peso máximo de decolagem de um avião Boeing 777-200ER é de 298.000 quilogramas, que também pode ser escrito como 2,98 × 10⁵ kg (298 toneladas). Já a massa de um mosquito médio é de cerca de 0,0000025 kg, que pode ser escrita como 2,5 × 10⁻⁶ kg.

Unidades em geral, como litros, libras e centímetros, são padrões de comparação para medições. Uma garrafa de 2 litros de refrigerante contém um volume de bebida que é o dobro do volume aceito de 1 litro. A carne usada para preparar um hambúrguer de 0,25 quilo pesa um quarto do peso aceito de 1 quilo. Sem unidades, um número pode ser sem sentido, confuso ou possivelmente fatal.

Suponha que um médico prescreva o medicamento fenobarbital para controlar as convulsões de um paciente e declare uma dosagem de “100” sem especificar unidades. Isso não só será confuso para o profissional médico que administra a dose, mas as consequências podem ser terríveis: 100 mg administrados três vezes ao dia podem ser eficazes como anticonvulsivante, mas uma única dose de 100 g é mais do que 10 vezes a quantidade letal.

As unidades de medida para sete propriedades fundamentais (“unidades básicas”) estão listadas na tabela a seguir. Os padrões para essas unidades são fixados por acordos internacionais e são chamados de Sistema Internacional de Unidades ou Unidades do SI (do francês, Le Système International d’Unités). As unidades do SI têm sido usadas pelo Instituto Nacional de Padrões e Tecnologia dos Estados Unidos (NIST) desde 1964 e são amplamente usadas no Brasil. As unidades para inúmeras outras propriedades podem ser derivadas dessas sete unidades básicas.

Unidades Base do Sistema Internacional (SI)
Medida	Unidade	Símbolo
Comprimento	Metro	m
Massa	Quilograma	kg
Tempo	Segundo	s
Temperatura Termodinâmica	Kelvin	K
Corrente Elétrica	Ampère	A
Quantidade de Substância	Mol	mol
Intensidade Luminosa	Candela	cd

As unidades de medida do dia-a-dia são frequentemente definidas como frações ou múltiplos de outras unidades. O leite é comumente embalado em recipientes de 1 galão (4 quartos), 1 litro (0,25 galão) e um litro (0,5 litro). Essa mesma abordagem é usada com unidades do SI, mas essas frações ou múltiplos são sempre potências de 10. As unidades do SI fracionárias ou múltiplas são nomeadas usando um prefixo e o nome da unidade base. Por exemplo, um comprimento de 1000 metros também é chamado de quilômetro porque o prefixo quilo significa “mil”, que em notação científica é 10³ (1 quilômetro = 1000 m = 10³ m).

Alguns dos prefixos usados e as potências às quais o valor 10 é elevado estão listados na tabela a seguir.

Prefixos Comuns de Unidades
Prefixo	Símbolo	Multiplicador	Exemplo
tera	T	1012	5 terawatts (TW) = 5 × 1012 W (5.000.000.000.000 W)
giga	G	109	8 gigaanos (Ga) = 8 × 109 anos (8.000.000.000 anos)
mega	M	106	3 megahertz (MHz) = 3 × 106 Hz (3.000.000 Hz)
kilo	k	103	1 kilômetro (km) = 1 × 103 m (1000 m)
deci	d	10-1	1 decilitro (dL) = 1 × 10−1 L (0,1 L )
centi	c	10-2	7 centímetro (cm) = 7 × 10−2 m (0,07 m)
mili	m	10-3	3,5 millimols (mmol) = 3,5 × 10−3 mol (0,0035 mol)
micro	μ	10-6	70 microgramas (μg) = 7 × 10−5 g (0,00007 g)
nano	n	10-9	4 nanogramas (ng) = 4 × 10−9 g (0,000000004 g)
pico	p	10-12	1 picômetro (pm) = 1 × 10−12 m (0,000000000001 m)
femto	f	10-15	1 femtosegundo (fs) = 1 × 10−15 s (0,000000000000001 s)

Unidades Base do SI

As unidades iniciais do sistema métrico, que eventualmente evoluíram para o sistema SI, foram estabelecidas na França durante a Revolução Francesa. Os padrões originais para o metro e o quilograma foram adotados em 1799 e posteriormente por outros países. Esta seção apresenta quatro das unidades de base do SI comumente usadas em química. Outras unidades SI serão apresentadas em artigos subsequentes.

Comprimento

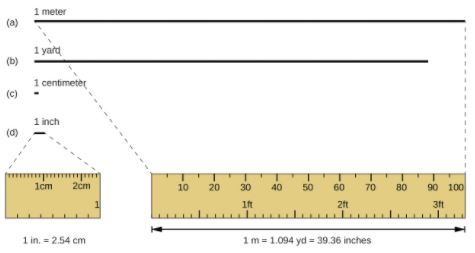
A unidade padrão de comprimento tanto no SI quanto no sistema métrico original é o metro (m). Um metro foi originalmente especificado como sendo 1 / 10.000.000 da distância do Pólo Norte ao equador. Ele agora é definido como a distância que a luz no vácuo viaja em 1 / 299.792.458 de segundo. Um metro é cerca de 3 polegadas maior do que uma jarda (sistema americano); um metro equivale a cerca de 39,37 polegadas ou 1,094 jardas. Distâncias mais longas são frequentemente relatadas em quilômetros (1 km = 1000 m = 10³ m), enquanto distâncias mais curtas podem ser relatadas em centímetros (1 cm = 0,01 m = 10⁻² m) ou milímetros (1 mm = 0,001 m = 10⁻³ m).

Massa

A unidade padrão de massa no sistema SI é o quilograma (kg). O quilograma foi previamente definido pela União Internacional de Química Pura e Aplicada (IUPAC) como a massa de um objeto de referência específico. Este objeto era originalmente um litro de água pura e, mais recentemente, era um cilindro de metal feito de uma liga de platina-irídio com altura e diâmetro de 39 mm.

Em maio de 2019, essa definição foi alterada para uma que é baseada em valores precisamente medidos de várias constantes físicas fundamentais. Um quilograma equivale a cerca de 2,2 libras. O grama (g) é exatamente igual a 1/1000 da massa do quilograma (10⁻³ kg).

Temperatura

A temperatura é uma propriedade intensiva (que não depende da quantidade do material). A unidade no SI de temperatura é o Kelvin (K). A convenção da IUPAC é usar kelvin (com todas as letras minúsculas) para a palavra, K (letra maiúscula) para o símbolo da unidade e não usar nem a palavra “grau” nem o símbolo de grau (°). O grau Celsius (° C) também é permitido no sistema SI, com a palavra “grau” e o símbolo de grau usados ​​para representar medições em Celsius. Os graus Celsius têm a mesma magnitude que os de Kelvin (centígrados), mas as duas escalas colocam seus zeros em lugares diferentes. A água congela a 273,15 K (0 °C) e ferve a 373,15 K (100 °C) por definição, e a temperatura normal do corpo humano é de aproximadamente 310 K (37 °C). O zero na escala kelvin é a menor temperatura possível (teórica) no Universo (zero absoluto)

A conversão entre essas duas unidades e a escala Fahrenheit será discutida posteriormente em outro artigo.

Tempo

A unidade de tempo base do SI é o segundo (s). Intervalos de tempo pequenos e grandes podem ser expressos com os prefixos apropriados; por exemplo, 3 microssegundos = 0,000003 s = 3 × 10⁻⁶ e 5 megasegundos = 5.000.000 s = 5 × 10⁶ s. Alternativamente, horas, dias e anos podem ser usados.

Unidades do SI derivadas

Podemos derivar muitas unidades das sete unidades básicas do SI. Por exemplo, podemos usar a unidade básica de comprimento para definir uma unidade de volume e as unidades básicas de massa e comprimento para definir uma unidade de densidade.

Volume

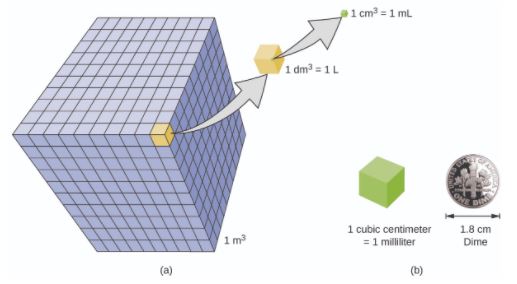
O volume é a medida da quantidade de espaço ocupado por um objeto. A unidade padrão de volume do SI é definida pela unidade básica de comprimento. O volume padrão é um metro cúbico (m³), que corresponde a um cubo com um comprimento de lado de exatamente um metro. Para dispensar um metro cúbico de água, poderíamos construir uma caixa cúbica com comprimentos de lado de exatamente um metro. Essa caixa comportaria um metro cúbico de água ou de qualquer outra substância.

Uma unidade de volume mais comumente usada é derivada do decímetro (0,1 m ou 10 cm). Um cubo com comprimentos de aresta de exatamente um decímetro contém um volume de um decímetro cúbico (dm³). Um litro (L) é o nome mais comum para o decímetro cúbico.

Um centímetro cúbico (cm³) é o volume de um cubo com tamanho de de exatamente um centímetro. A abreviatura cc (para centímetro cúbico) é freqüentemente usada por profissionais de saúde, por exemplo na expressão 5 cc de dipirona (5 cm³ ou mL de dipirona). Um centímetro cúbico é equivalente a um mililitro (mL) e equivale a 1/1000 de um litro.

Densidade

Usamos a massa e o volume de uma substância para determinar sua densidade. Assim, as unidades de densidade são definidas pelas unidades básicas de massa e comprimento.

A densidade de uma substância é a relação entre a massa de uma amostra da substância e o seu volume. A unidade SI para a densidade é o quilograma por metro cúbico (kg/m³). Para muitas situações, no entanto, essa é uma unidade inconveniente, por se tratar de um valor grande, e geralmente usamos gramas por centímetro cúbico (g/cm³) para as densidades de sólidos e líquidos e gramas por litro (g/L) para densidades de gases.

Embora haja exceções, a maioria dos líquidos e sólidos tem densidades que variam de cerca de 0,7 g/cm³ (densidade da gasolina, uma mistura de hidrocarbonetos leves) a 19,25 g/cm³ (densidade do tungstênio). A densidade do ar é de cerca de 1,2 g/L.

A Tabela a seguir mostra as densidades de algumas substâncias comuns.

Densidades de algumas substâncias comuns
Sólidos	Líquidos	Gases
gelo (a 0 °C): 0,92 g/cm3	água: 1,0 g/cm3	ar seco: 1,20 g/L
carvalho (madeira): 0,60 a 0,90 g/cm3	etanol: 0,79 g/cm3	oxigênio: 1,31 g/L
ferro: 7,9 g/cm3	acetona: 0,79 g/cm3	nitrogênio: 1,14 g/L
cobre: 9,0 g/cm3	glicerina: 1,26 g/cm3	dióxido de carbono: 1,80 g/L
chumbo: 11,3 g/cm3	azeite de oliva: 0,92 g/cm3	hélio: 0,16 g/L
prata: 10,5 g/cm3	gasolina: 0,70 a 0,77 g/cm3	gás neônio: 0,83 g/L
ouro: 19,3 g/cm3	mercúrio: 13,6 g/cm3	radônio: 9,1 g/L

Embora existam muitas maneiras de determinar a densidade de um objeto, e talvez o método mais simples envolva encontrar separadamente a massa e o volume do objeto e, em seguida, dividir a massa da amostra por seu volume.

Fórmula da densidade:

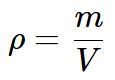
onde:

• ρ (letra grega rho) é a densidade (ocasionalmente é representada pela letra D)
• m é a massa da substância
• V é o volume

Exemplo de Cálculo de densidade

O ouro – em tijolos, barras e moedas – é usado como valor monetário há séculos. A fim de enganar as pessoas para que paguem por uma barra de ouro sem realmente levar uma barra de ouro, fraudadores costumam rechear os centros de barras ocas de ouro com chumbo para tentar enganar os compradores e fazê-los pensar que a barra inteira é de ouro. Mas isso não funciona: o chumbo é uma substância densa, mas sua densidade não é tão grande quanto a do ouro, que é de 19,3 g/cm³.

Pergunta-se: qual é a densidade do chumbo se um cubo de chumbo tem um comprimento de aresta de 2,00 cm e uma massa de 90,7 g?

Solução
A densidade de uma substância pode ser calculada dividindo sua massa por seu volume. O volume de um cubo é calculado ao elevar o comprimento da borda ao “cubo”.

volume do cubo de chumbo = 2,00 cm × 2,00 cm × 2,00 cm = 8,00 cm³

Assim, temos que:

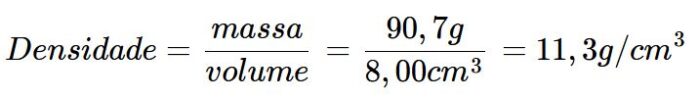
Portanto, a densidade do chumbo é de 11,3 g/cm³ – bem menor do que a do ouro, apesar de ser alta!

Nos próximos artigos vamos falar sobre algarismos significativos, precisão, arredondamento de valores e notação científica.

Referências

Unidades de Medida e o Sistema Internacional de Unidades – Canal Bóson Ciências:

Livro Recomendado: